Category: Mathematics

IEEE 754 Subnormal Numbers are your Friend

On August 1, 2025

Most programmers use floating-point numbers without a second thought. Data types such as float and double are widely available in programming languages. Some languages hide the actual representation and perform conversions in the background. The basis of floating-point variables and how to do operations on them is defined in the IEEE Standard for Floating-Point Arithmetic (IEEE 754) document. It’s worthwhile to learn some basics about what IEEE 754 does for you. It is also important to know that there are special numbers such as +0, -0, infinity, not-a-number, and subnormal numbers. Usually everything just works, but there are special cases where you need to be careful when doing numerical calculations. The division by zero error/exception is a famous example. I want to focus on the subnormal numbers to explain why this kind of numbers were introduced into the standard.

Computing the difference between two numbers can lead to very small numbers. What are the limits of small differences? The C library helps you out by defining the constant FLT_EPSILON (defined in cfloat or float.h). Before IEEE 754 calculations would something lead to 0 when the differences became too small. Subnormal numbers help you out. When enabled, floating-point operations cannot underflow. All absolute differences between two numbers a and b are always positive. This essentially protects you from accidentally dividing by zero. Unless a and b are equal, you are safe. Compilers and processors allow you to disable subnormal numbers. For compilers, there are the -Ofast and -ffast-math flags. It is tempting to use them, but this won’t make your code magically faster. Processors have similar options in the shape of the “flush to zero” (FTZ) and “denormals-are-zero” (DAZ). Intel® has documented FTZ and DAZ. AMD™ and ARM CPUs have the same of similar flags. Enabling FTZ or DAZ sets all subnormal numbers to zero. Why would one want to disable these numbers? Well, subnormal numbers are slower to computer and can affect the performance. This is the reason why -Ofast and -ffast-math set the FTZ/DAZ flags.

Why is this important? It depends a lot of what calculations you do. If you never divide by the difference between two numbers, you are probably fine. The trick is to know if this is the case. You would need to inspect all mathematical operations and track all floating-point variables. There is also a catch. Setting FTZ/DAZ disables subnormal numbers for all code instructions in your process. This includes calling library functions. If components do not expect a change in behaviour regarding floating-point operations, then there can be additional errors or effects. You are not immune if you use a higher-level programming language. There is a blog article where the subnormal number deactivation impacted Python code. There is also an article with a simple example how things can go wrong (examples for C# and C++).

If you are not sure if this affects your code, try running it with and without subnormal numbers. The authors of IEEE 754 recommend not disabling them for very good reasons. I recommend reading the interview with William Kahan about why the proposal for subnormal numbers was added to the standard.

Static Tests and Code Coverage

By René Pfeiffer

On September 17, 2024

In Development, Mathematics, Testing

Testing software and measuring the code coverage is a critical ritual for most software development teams. The more code lines you cover, the better the results. Right? Well, yes, and no. Testing is fine, but you should not get excited about maximising the code coverage. Measuring code coverage can turn into a game and a quest for the highest score. Applying statistics to computer science can show you how many code paths your tests need to cover. Imagine that you have a piece of code containing 32 if()/else() statements. Testing all branches means you will have to run through 4,294,967,296 different combinations. Now add some loops, function calls, and additional if() statements (because 32 comparisons are quite low for a sufficiently big code base). This will increase the paths considerably. Multiply the number by the time needed to complete a test run. This shows that tests are limited by physics and mathematics.

Static analysis is a standard tool which helps you detect bugs and problems in your code. Remember that all testing tries to determine the behaviour of your application. Mathematics has more bad news for you. Rice’s Theorem states that all non-trivial semantic properties of a specific code are undecidable. An undecidable problem, which is a decision problem, cannot be solved by any algorithm implementation. Rice published the theorem with a proof in 1951, and it relates to the halting problem. It implies that you cannot decide if an application is correct. You also cannot decide if the code executes without errors. The theorem sounds odd, because clearly you can run code and see if it shows any errors given a specific set of input data. This is a special case. Rice’s theorem is a generalisation and applies to all possible input data. So your successful tests basically work with special cases that do not cause harm. Security testing checks for dangerous behaviour or signs of weaknesses. Increasing the input data variations can cover more cases, but Rice’s theorem still holds, no matter how much effort you put into your testing pipeline.

Let’s get back to the code coverage metric. Of course, you should test all of your code. The major goal for your code is to handle errors correctly, fail safely (i.e. without creating damage), and keep control of the code execution. You can achive these goals with any code coverage per test above 0%. Don’t fall prey to gamification!

Floating Point Data Types and Computations

By René Pfeiffer

On May 7, 2024

In C/C++, Data, Mathematics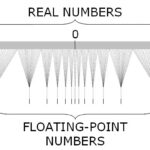

Floating point data types are available in most programming languages. C++ knows about float, double, and long double data types. Other programming languages feature longer (256 bit) and shorter (16 bit and lower) representations. All data types are specified in the IEEE Standard for Floating-Point Arithmetic (IEEE 754). IEEE 754 is the standard for all implementations. Hardware also supports storage and operations. Floating point data storage is usually used in numerical calculations. Since the use case is to represent real numbers, the accuracy is a problem. Mathematically there is an infinite amount of other real numbers between two arbitrary chosen real numbers. Computers are notoriously bad at storing an infinite amount of data. For the purposes of programming, this means that all choices for using any floating point data type have to deal with error conditions and how to handle them. Obvious errors include the division by zero. Less obvious conditions are rounding errors, special numbers (infinity, not a number, signed zeroes, subnormal numbers), and overflows.

Not all of the error conditions may pose a threat for your applications. It depends on what type of numerical calculations your code does or consumes. Comparisons have to be implemented in a thoughtful way. Test for equality may fail, because of rounding errors. Using the “real zero” can backfire. The C and C++ standard libraries supply you with a list of constants. Among them is the minimal difference that can be represented in a floating point data type. It is called the epsilon value. Epsilon (ε) is often used to denote very small values. cfloat or float.h defines FLT_EPSILON (for float), DBL_EPSILON (for double), and LDBL_EPSILON (for long double). Using this value as the smallest difference possible is usually a good idea. There is another method for finding neighbouring floating point numbers. C++11 has introduced functions to find the next neighbour value. The accuracy is determined by the unit of least precision (ULP). ULPs are defined by the value of the least significant bit. Using ULPs or the epsilon values is a different approach. ULP checking requires transformation of the values into integer registers. Both methods work well away from the zero. If you are near the zero value, then consider using multiples of the epsilon value as a comparison value.

There is another overlooked fact. The float data type has 32 bit of storage. This means you can use 4 billions different bit combinations, which is not a lot. Looping through all values and stress testing a numerical function can be done in minutes. There is a blog post covering this technique complete with example code.

I have compiled some useful resources for this topic.